+7 (495) 280-02-06
info@butis.ruАнализируются базовые модели дельта-функций, эквивалентных схем и Р-матриц фильтров на поверхностных акустических волнах (ПАВ) на СВЧ. На их основе разработано программное обеспечение для расчета всех типов базовых конструкций фильтров на ПАВ с высокой входной мощностью для систем специальной связи, радиолокационной и телекоммуникационной аппаратуры.
Важнейшей задачей при разработке любого устройства на поверхностных акустических волнах (ПАВ) является точность моделирования элементов, входящих в его структуру. Поскольку встречно-штыревые преобразователи (ВШП) являются основными элементами любого фильтра на ПАВ, очень важно иметь адекватную физическую модель преобразователя. До середины 1980-х годов основными методами расчета преобразователей с малым уровнем отражений были модель дельта-функций [1] и квазистатическое приближение [2]. Серьезным преимуществом первой модели является то, что на частотные свойства ВШП решающее влияние оказывают только его периодичность, число δ-источников и распределение максимального значения интенсивности источников, а не закон распределения электроупругого поля. Второй метод, основанный на использовании функции Грина для описания поверхностного потенциала, является более точным.
Данные методы обеспечивают удовлетворительную сходимость результатов при расчете трансверсальных фильтров различных методов взвешивания и конструкций [3]. Однако они непригодны для анализа структур с ненулевым уровнем отражений, на которых обычно реализуются ПАВ-фильтры с малыми потерями: на основе продольно-связанных резонаторных структур [4], на основе U-образного [5] и реверсивного [6] многополосковых ответвителей, структур импедансного типа [7,8], поскольку в них не учитываются влияние массовой нагрузки и эффект электрического закорачивания поля.
Необходимость расчета структур, работающих на основе внутренних отражений, обусловила необходимость разработки двумерной физической модели, учитывающей влияние масс-электрического нагружения на характеристику преобразователя [9]. Математический анализ таких структур до последнего времени был связан с большими трудностями, поскольку для точного моделирования характеристик требовался учет различных вторичных факторов. Использование теории связанных мод (coupling-of-modes-COM) для анализа преобразователей ПАВ, впервые предложенной К. Хартманом [10] и В. Райтом [11] и получившей развитие в работах советских, а затем российских авторов, существенно упростило задачу. Основными достоинствами этой модели являются простая математическая интерпретация, точное моделирование эффектов отражения внутри преобразователя, отказ от использования модели эквивалентной цепи при расчете параметров ВШП.
Данные методы использованы для разработки САПР фильтров на ПАВ любой сложности на разных стадиях этапа проектирования [12,13].
Предварительный анализ фильтров на ПАВ осуществляется с использованием модели δ-функций. Материал подложки, эффекты второго порядка, пространственная протяженность электродов и т.д. в данной модели не учитываются.
В простейшем случае фильтр на ПАВ состоит из двух встречно-штыревых преобразователей – входного и выходного. Источником ПАВ является зазор между соседними электродами. Перекрытие между соседними электродами называется весом источника. Каждому источнику ПАВ ставится в соответствие δ-импульс, расположенный в центре источника и умноженный на соответствующий вес (весовой коэффициент).
Модель основана на использовании прямого (1) и обратного (2) дискретного преобразования Фурье (ДПФ и ОДПФ).
где s(n) - n-й весовой коэффициент.
Выражение для ДПФ ставит в соответствие N отсчетам сигнала s(n) N отсчетов спектра S(k).
Амплитудно-частотную характеристику (АЧХ) ВШП можно получить при помощи модифицированного прямого дискретного преобразования Фурье:
где fi – текущая частота; f0 – центральная частота ВШП; S(fi) – комплексная передаточная функция ВШП на текущей частоте.
АЧХ H(fi)=|S(fi)|или в децибелах 20lg|S(fi)|.
Фаза φ(fi) = arg (S(fi)) сигнала равна аргументу комплексного числа.
Групповое время запаздывания (ГВЗ)
Модель дельта-функций обычно используется на начальном этапе разработки устройства на ПАВ.
В качестве базовой модели для анализа фильтров на ПАВ, в том числе на материалах с естественной однонаправленностью, используется модель эквивалентных схем. В этой модели ВШП разбивается на элементарные ячейки, каждая из которых описывает фрагмент звукопровода между центрами соседних электродов (рис.1).
Каждая элементарная ячейка представляется в виде эквивалентной схемы шестиполюсника, которая описывается матрицей размерности 3×3, связывающей токи и напряжения структуры. Элементы матрицы элементарной ячейки определяются по правилам расчета электрических цепей, исходя из электрофизических свойств материала звукопровода:
где Z − характеристическое сопротивление среды для свободной и металлизированной Z = Zim поверхностей; θ – угол, на который смещается фаза волны за время прохождения участка; r − коэффициент трансформации, описывающий преобразование электрического сигнала в акустическую волну и наоборот.
Комплексная проводимость B = ReB + Im B позволяет учесть эффекты второго порядка, такие как рассеяние (определяется значением ReB) и накопление энергии (ImB) на границе металл – свободная поверхность. Коэффициент отражения волны на границе может быть рассчитан по формуле:
Указанные эффекты второго порядка, как правило, зависят от относительной толщины электродов, т.е. являются частотно-зависимыми. В модели эти зависимости описываются полиномами. Например, полиномы, передающие эффекты отражения, распространения и накопление энергии, имеют вид
где λ − текущая длина волны; h − толщина электродного покрытия.
Коэффициенты полиномов определяются для различных материалов и типов волн, как правило, экспериментальным путем по результатам испытаний тестовых устройств.
После вычисления матриц шестиполюсников каждой элементарной ячейки для заданного частотного диапазона эти матрицы последовательно сворачиваются (перемножаются). В результате получается матрица комплексных проводимостей фильтра:
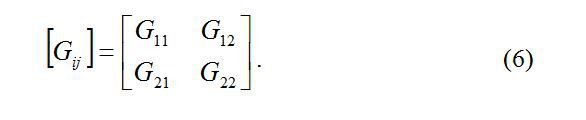
Комплексная передаточная функция K может быть найдена по формуле
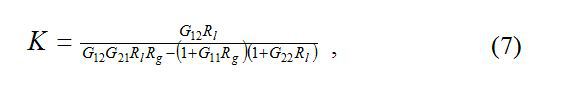
где Rl и Rg− сопротивление нагрузки и источника сигнала соответственно.
Зная передаточную функцию, можно найти комплексную АЧХ фильтра:
а также фазу и характеристику группового времени замедления (ГВЗ).
Преимущество данной модели перед аналогичными моделями состоит в том, что эквивалентные параметры базовых ячеек определяются положением границ электродов. Это позволяет моделировать электродные структуры произвольной конфигурации. Такая гибкость модели обеспечивает возможность ее применения при синтезе различных типов ВШП.
В основе СОМ-метода [14], предложенного К.Хартманом и В.Райтом используется ряд допущений. Так, при анализе рассматривается преобразователь с малым уровнем потерь, имеющий равномерную структуру и одинаковую величину перекрытия электродов (рис.2). Также, для упрощения, вводится допущение, что уровень переотражений мал. Тогда, дифференциальные СОМ-уравнения, описывающие распространение волны в электродной структуре, имеют вид:
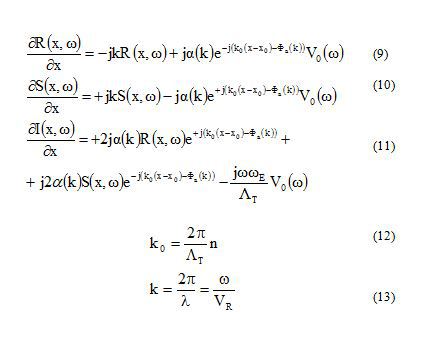
СОМ-переменными являются: R(x, ω)- поверхностная волна в прямом направлении, S(x, ω) - поверхностная волна в обратном направлении, V0(ω) - потенциал преобразователя и I(x, ω) - ток в подводящих шинах. Тогда как СОМ-параметры это: α(k) - амплитуда преобразования, Фα(k)- фаза преобразования, ΛТ - период преобразователя, L - длина преобразователя, CE - электростатическая емкость на период преобразователя, ω - круговая частота, λ - длина волны ПАВ, VR - фазовая скорость волны. X0 - это начальная точка отсчета по оси Х, k0 - волновое число, n - номер гармоники. Обычно СОМ-анализ проводят для фундаментальной моды, что соответствует n=1.
Решение системы дифференциальных уравнений (9-11) может быть найдено при выполнении условия:
Представляет интерес использование Р-матриц для решения СОМ-уравнений. При этом акустические порты рассматриваются как порты отражения, а электрический порт совпадает с адмитансным. Как показано на рис.2, акустические порты расположены на краях преобразователя с координатами для левого порта и для правого порта. Поскольку электрический порт расположен на левом краю преобразователя, то ток в преобразователе привязан к координате . Р-матрица показывает связь выходящих акустических волн и тока с входящими акустическими волнами и потенциалом преобразователя:
При записи решений СОМ-уравнений удобно ввести величину, показывающую отстройку от центральной частоты волнового вектора:
Тогда решение матрицы проводимости для однородного преобразователя с малым уровнем внутренних отражений имеет вид:
Поскольку ПАВ-фильтры с малым вносимым затуханием в основном реализуются на сильных пьезоэлектриках, для которых уровень переотражений не равен нулю, то дальнейшее развитие СОМ-теории было связано с определением коэффициентов отражения (P11) и пропускания (P12) преобразователя, как функции коэффициента отражения от электрода [15]:
где параметр Δ определяет частотную отстройку относительно центральной частоты ωс, k – коэффициент отражения от пары электродов, а L – длина отражающей структуры.
Развитие аппаратуры передачи, обработки и приема информации нового поколения существенно ужесточило требования к таким параметрам ПАВ-фильтров как уровень вносимого затухания и прямоугольность АЧХ, и как следствие, привело к усложнению исходной модели преобразователя ПАВ. Например, в работе [16] учтена дисперсия скорости волны от частоты и потери на распространение γp.
В последние годы для анализа прецизионных высокоизбирательных фильтров на ПАВ с малым вносимым затуханием используется модифицированный СОМ-метод, в котором параметры структуры на ПАВ в целом (ВШП, отражающей структуры или их произвольной комбинации) определяются перемножением соответствующих Р-матриц отдельных электродов (как это делается в обычной теории четырехполюсников с использованием матрицы рассеяния) [17]. Этот метод позволяет учитывать изменяющийся период структуры, аподизацию и неоднородное распределение поверхностного заряда на электродах структуры и он более перспективен с точки зрения дальнейшего усложнения исходной модели структуры.
Пусть задана ПАВ-структура в виде электродов с чередующейся полярностью, произвольно меняющимся периодом и перекрытием соседних электродов. Также предполагаем, что источник сигнала U0 подключен слева. Рассмотрим k-й электрод ВШП (рис. 3). Пусть R(Z,w) и S(Z,w) – две связанные между собой плоские волны с волновым числом k, распространяющиеся в электродной структуре ВШП. Причем R(Z,w) распространяется в направлении оси Z, а S(Z,w) – в направлении, противоположном оси Z. Тогда однородные плоские волны можно записать в виде
где R(w) и S(w) – комплексные амплитуды соответствующих волн.
Пусть на k-й электрод слева падает волна RK(R,w), а справа – SK+1(Z,w). Тогда для комплексных амплитуд прошедших волн с учетом механизмов отражения, прохождения и преобразования с коэффициентом εK можно получить уравнения
Фазовые сомножители у слагаемых, связанных с отражением (преобразованием) волн, определяют фазовый набег от центра отражения (преобразования) волны до соответствующей границы: ZK – для SK(w) и ZK+1 - для RK(w). Центр отражения (преобразования) ПАВ принят находящимся в центре электрода. Вычислим эффективное волновое число:
где rK – комплексный коэффициент отражения от k-го электрода; kЕ – эффективное волновое число ПАВ; k0 = 2p/pK; pK= ZK+1–ZK; xK – коэффициент преобразования ПАВ на k-м электроде; h1K=W1K/W0; h2K=W2K/W0; W0 – максимальная апертура; W1K – перекрытие соседних электродов; W2K=W0 в случае, если используются холостые электроды; W2K=W1K, если холостые электроды не используются.
kЕ = 2p / lE=w /(V0 + LK (VM – V0)/pK) – ja,
где V0 – скорость ПАВ на свободной поверхности; VM – скорость ПАВ под металлизированной поверхностью; a – суммарные потери на распространение ПАВ в электродной структуре на единицу длины.
Изменение тока в шине ВШП происходит за счет преобразования прямой и обратной волн и падения напряжения на емкости электрода
Рассмотрим слагаемые, связанные с преобразованием ПАВ при прохождении через электрод ВШП (рис.3), с учетом того, что возбуждение носит распределенный характер. Будем полагать, что прямое и обратное преобразование волны на электродах происходит с одинаковой эффективностью, т.е. носит взаимный характер. Пусть задано распределение поверхностного тока на электродах ВШП в виде J(Z). Будем считать, что механизм преобразования ПАВ малым участком поверхностного тока DZK электрода и всего электрода аналогичны. Тогда, просуммировав вклады и преобразование ПАВ по ширине электрода относительно его центра ZCK и переходя к пределу (ΔZK→ 0), получим
Соотношения (24) – (26) можно записать в матричной форме:
где Ga– акустическая проводимость излучения на частоте синхронизма.
Используя систему уравнений (24)–(26) с произвольными коэффициентами, записанную для двух последовательно включенных ПАВ-структур, нетрудно получить компоненты суммарной P-матрицы:
Теперь P-матрица ВШП в целом может быть найдена последовательным перемножением P-матриц, описывающих каждый электрод.
где P0 = 1–P(2)(1,1) P(1)(2,2). Верхние индексы s, 1 и 2 относятся, соответственно, к суммарной P-матрице, Р-матрице ПАВ-структуры, находящейся слева, и Р-матрице ПАВ-структуры, находящейся справа.
ПАВ-структура может представлять собой отдельный электрод или группу электродов, для которой вычислена суммарная Р-матрица. При этом соотношения (29)–(37) позволяют рассчитывать входную проводимость P(3,3) ВШП в составе фильтра или резонатора с произвольно меняющимся периодом и апертурой электродов вдоль структуры ВШП и реальным распределением поверхностного тока (заряда) на электродах ВШП.
Для отражающих структур расчет компонентов Р-матрицы производится при выполнении условий, что xK= 0, U= 0 и С2 = 0. При этом элементы матрицы Р (1,3), Р(2,3), Р (3,1), Р (3,2), Р (3,3) будут равны нулю.
Р-матрица, описывающая зазор между ВШП и отражательной структурой, может быть получена из соотношений (24)–(26) при условиях xK= 0, U= 0 и С2 = 0, rK=0 и WK= 0. В этом случае ненулевыми будут только элементы Р-матрицы Р(1,2), Р(2,1). Учет фазовой задержки при распространении волны в зазоре осуществляется путем умножения амплитуд падающих и выходящих волн на exp(-jkd), где d – расстояние между ВШП и отражающей структурой. Расчет проводимости фильтра в целом осуществляется путем перемножения соответствующих Р-матриц и решения суммарной системы уравнений (28) относительно токов в преобразователях.
Данный подход был использован при разработке программного обеспечения для расчета всех типов базовых конструкций фильтров на ПАВ с высокой входной мощностью.
Приведенные базовые модели для расчета электродных структур позволяют рассчитать фильтры на ПАВ любой сложности, в том числе с ненулевым уровнем отражений. Исключение составляют трансверсальные фильтры с апертурой преобразователей менее 10 длин волн и резонаторные поперечно-связанные узкополосные ПАВ-фильтры, для точного расчета которых необходимо дополнительно учитывать эффекты волноводного распространения поверхностной акустической волны [18].