+7 (495) 280-02-06
info@butis.ruРассмотрены конструктивно-технологические особенности проектирования резонаторных ПАВ-фильтров на основе поперечно-связанных структур. Приведена методика расчета с использованием трехмерной СОМ-теории, позволяющая анализировать структуры с неравномерным характером распределения фронта волны вдоль апертуры преобразователя. Представлены экспериментальные результаты разработки фильтров на основе ST-среза кварца.
Впервые резонаторные волноводно-связанные ПАВ-фильтры были описаны Тайстеном в 1975 году [1]. Позднее К.Кэмбелл разработал модель эквивалентной схемы на основе теории связанных мод во времени и в пространстве [2]. В 1992 г. К.Хартманн [3] впервые рассчитал их частотную характеристику, используя принцип суперпозиции симметричной и антисимметричной мод, и экспериментально получил соответствующие СОМ-параметры на основе шестивходовой тестовой структуры.
В противоположность этой теории в работе [4] расчет частотной характеристики проведен на основе одномерной Р-матрицы путем разбиения фильтровой структуры на элементарные ячейки, определяющие задержки и положение центров возбуждения и отражения. В работе описан эффект накопления энергии и влияние механической нагрузки конечной толщины. Двумерная природа данной задачи учитывалась за счет введения форм-факторов, описывающих характер распределения профиля скорости волны, возбуждения и отражения вдоль апертуры преобразователя, рис.1.
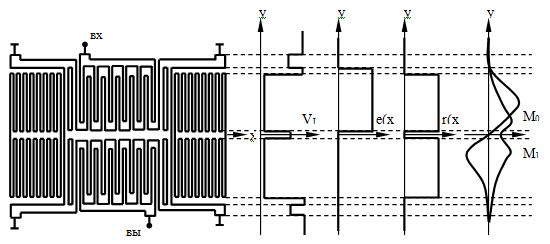
Рис.1. Структура двухвходного поперечно-связанного резонаторного фильтра и распределение скорости волны, ее возбуждения и отражения вдоль апертуры преобразователя. М0 и М1 обозначены основные симметричная и несимметричная моды, соответственно.
При этом моделирование характеристики распространения волны, ее возбуждение и отражение проводилось раздельно, а Р-матрица использовалась для сведения всех эффектов вместе. Этот подход позволил рассчитать передаточную функцию фильтра в общем виде на основе стандартных параметров материала и в дальнейшем применять его к расчету любых конструкций двухвходовых устройств.
Однако реальное ПАВ-устройство является трехмерной структурой. В работах [5-7] приведена методика расчета характеристик фильтров для такого случая, учитывающая только параметры материала и геометрию структуры. Эта методика менее точная, чем предыдущая, поскольку не учитывает ряд паразитных явлений, например, объемную составляющую волны. Тем не менее, она достаточно эффективна при расчете конкретной топологии фильтра на основе поперечно-связанной структуры. Разработка собственной теоретической модели для фильтров такого класса проводилась на основе последней методики, поскольку она позволяет проводить расчеты по достаточно простым математическим выражениям с использованием стандартных программ типа «MathCAD».
На рис.2 приведена конструкция исследуемого двухвходового резонаторного фильтра на основе поперечно-связанной структуры. Он содержит два идентичных ВШП, акустически соединенных параллельно, и две отражательных решетки. Зеркальная симметрия относительно оси Х является неотъемлемой особенностью данной структуры. Через lg и lт обозначены расстояния между центрами электродов в отражателе и преобразователе; Ng и Nт – соответствующее число электродов, а αg и αт – коэффициенты металлизации. Н – толщина металлизации в структуре. U – напряжение, приложенное к преобразователю. I – ток в преобразователе.
В работе [6] показано, что на поверхности кристалла электрический потенциал ПАВ, распространяющейся в двумерной периодической решетке, можно представить выражением:
где k=π/l; хо – координата центра любого электрода с нулевым потенциалом; R(x) и S(x) – медленно изменяющиеся комплексные амплитуды прямой и обратной волн. Зависимость амплитуд в продольном направлении Х и тока I(х) на единицу площади решетки описывается СОМ-уравнениями в виде:
со следующим рядом СОМ-параметров:
где U – приложенное напряжение (для закороченных электродов U=0); vо, vm и v– скорости ПАВ на свободной, металлизированной областях и в решетке на частоте синхронизма, соответственно; ε¥- эффективная диэлектрическая проницаемость при бесконечном волновом числе; а – потери на распространение; К – комплексный эллиптический интеграл первого рода и «*» - комплексное сопряжение. Коэффициенты De, Dm, Ds, Re, Rm – связаны с параметрами материала и определены в [6]. Временная зависимость определяется задержкой е-jwt, где w = 2pf, а f – текущая частота.
Дальнейший анализ проводится из условия, что структура делится на три области: 1 – переходная область шириной G, 2 – соответствует ширине преобразователя по апертуре W, где Wo – рабочая апертура преобразователя и 3 – металлизированные полубесконечные (для упрощения теории) области. Условия распространения ПАВ в этих областях для каждой поперечной секции слабо различаются. Это означает, что поле ПАВ в области 1 должно иметь слабую зависимость от координаты Y. Эта зависимость вводится в выражение для медленно меняющихся амплитуд с помощью дополнительного множителя Ψ(y). Кроме того, учитывается, что в структуре может существовать несколько мод:
где сумма учитывает все возможные моды; m – число мод, а все безразмерные функции Ψ(y) – действительные и ортогональные со следующей нормировкой:
где δmn – символ Кронекера ранга 2, равный 1 при m=n и нулю во всех других случаях.
Необходимо определить напряжения в У-направлении:
Следует отметить, что в области отражателя напряжение также равно нулю.
СОМ-уравнения (2)-(4) выведены для двумерной структуры. Для решения трехмерной задачи предположим, что они справедливы для конкретного значения «у». Кроме того, предположим, что коэффициенты (5) и (6) (за исключением А1) определяются только в области перекрытия электродов и равны нулю во всех других областях. Коэффициент А1 имеет два значения, которые определяются в основном значениями скорости ПАВ для областей 1,3 и 2. Тогда, подставляя в (2)-(4) выражения (8)-(10) и интегрируя по «у» от -¥ до +¥, имеем систему уравнений для амплитуд всех возможных мод в структуре (симметричных и несимметричных). При этом изменение коэффициента преобразования вдоль оси «у» в рабочей зоне преобразователя определяется безразмерным параметром Θn,:
Аналогичная процедура проводится для уравнения (4). Тогда с учетом (11) и интегрирования (4) вдоль апертуры Wо в каждой области ВШП имеем выражения для токов i1 и i2 на единицу длины вдоль оси Х в верхнем и нижнем каналах структуры:
где знак «+» соответствует симметричной моде, а «-» – антисимметричной моды. Интегрирование уравнений (12), (13) вдоль направления Х позволяет получить выражения для общих токов I1 и I2 в верхнем и нижнем ВШП с учетом возникновения симметричной и несимметричной мод:
где ток для каждой моды равен:
или, вводя понятие « полный адмитанс системы» Yn:
Совместное решение системы уравнений для токов и амплитуд волны позволяет получить Р-матрицу проводимости для поперечно-связанной структуры преобразователей [7]:
где L – длина преобразователя.
Проведя аналогичные преобразования для отражательной решетки и учитывая, что напряжение в ней равно нулю, имеем полный адмитанс системы:
Индексы «Т» и «G» у элементов Р-матрицы соответствуют ВШП или отражателям. Ф – определяет фазовую задержку между ВШП и отражателями.
Входящий в выражения (19) коэффициент А1 имеет значение фазовой задержки на единицу длины и зависит от скорости моды ПАВ в решетке на частоте синхронизма, которая в свою очередь определяется характером Ψn для каждой моды.
Коэффициент А2 определяет отражение волны от электрода на поверхности пьезоэлектрика. Поскольку данный тип конструкций рассчитан в основном на использование STX-кварца в качестве пьезоподложки, то в данной работе была получена аналитическая зависимость коэффициента отражения R для данного материала от толщины металлизации и коэффициента металлизации (рис.3) на основе экспериментальных данных, приведенных в [8]:
где R - коэффициент отражения на длину волны; dVv - коэффициент электромеханической связи; Ps - функции Лежандра, где s определяет тип электродной структуры (количество электродов на период); Δ - коэффициент металлизации в структуре; hλ- толщина пленки алюминия в длинах волн; ε – диэлектрическая проницаемость; а – числовой коэффициент. Использование данной зависимости при расчете реального фильтра дали хорошую сходимость результатов.
Для определения зависимости скорости ПАВ от величины апертуры преобразователя были использованы основные теоретические выводы по волноводному распространению волны, полученные авторами ранее в работах [9-12].

Рис.3. Зависимость коэффициента отражения R от относительной толщины Hl и коэффициента металлизации Δ для STX – кварца
Эффект волноводного распространения волны в электродной структуре возможен только при условии, что скорость волны в данной области меньше скорости волны за ее пределами. Практическая реализация таких структур на пьезоэлектриках с сильной или средней пьезоактивностью (например, 64°- или 128°- срезы ниобата лития) требует использования узких шин в преобразователях – не более длины волны, либо формирования «окон» в этих шинах. При рассмотрении слабых пьезоэлектриков, таких как STX-кварц, можно применить несколько другой подход для решения данной задачи. Так из анализа уравнения для скорости волны (7) ясно, что такое соотношение скоростей можно получить только путем исключения квадратичного члена для областей 1,3 рис.2, который вводится в основном для учета краевых эффектов на электродах:
Как показано в работе [6], коэффициент Ds(α,Н) логарифмически зависит от величины Н и для малых изменений его можно считать постоянным. При этом его абсолютная величина для структуры алюминиевая пленка/STХ-кварц равна 9 [7]. На рис.4 приведены характеристики скорости волны, рассчитанные по уравнениям (22), (23) для коэффициента металлизации 0,5. Из графика видно, что только для случая Н/λ> 0,9% может возникать волноводный эффект.
Решение скалярного волнового уравнения получается из рассмотрения граничных условий для скалярных потенциалов между областями с быстрой и медленной скоростями:
где Вi– произвольные константы, а волновые числа κ определяются как:
где l – расстояние между электродами в конкретной решетке.
Тогда совместное решение (24), (25) для граничных точек дает дисперсионное соотношение для двух типов мод (26):
где tanh соответствует симметричной моде, coth – несимметричной, а m - определяет порядок моды.
Дальнейшие преобразования выражений (24), (25) с учетом (9), (11) и полученных значений скорости υ позволяет определить параметр Θ как функцию апертуры преобразователей W. Таким образом, определены все параметры, входящие в выражение (21) для полного адмитанса фильтра на основе поперечно-связанной структуры.
Разработка программного обеспечения проводилась в соответствии с данными выводами, причем была предусмотрена возможность каскадирования таких структур, что важно для реализации большого гарантированного затухания фильтра в полосах заграждения (более 50 дБ). Входными параметрами программы являются: параметры материала звукопровода (коэффициент связи, диэлектрическая проницаемость, коэффициент затухания ПАВ при распространении), скорость на свободной поверхности и коэффициент отражения в структурах, а также геометрия конструкции (число штырей в преобразователях и отражателях, апертура, коэффициент металлизации, величина зазоров между ВШП и отражателями, величина переходной области в связанных преобразователях).
Для подтверждения результатов данного теоретического анализа был изготовлен фильтр на частоту 167,8 МГц со следующими геометрическими параметрами. Преобразователи и отражатели содержали 801 и 300 одинарных электродов, соответственно; величина переходной зоны не превышала длину волны и составляла 12 мкм; для согласования с нагрузкой 50 Ом была выбрана рабочая апертура 17λ; коэффициент металлизации был равен 0,55; толщина металлизации составляла 0,27 мкм..
Для этих параметров структуры существует только две основных моды: симметричная и несимметричная, что соответствует случаю m=0 в уравнении (26). Для обеспечения минимального вносимого затухания преобразователь и отражатель были сведены на близкие частоты, при этом их длины волн различались в 1,002 раза. На рис.5 приведены основные расчетные характеристики преобразователя и отражателя для данной топологии.
Использование одинаковых периодов в структурах приводит к сильному искажению характеристики в полосе пропускания, рис.6, что обусловлено изменением характера продольной моды.
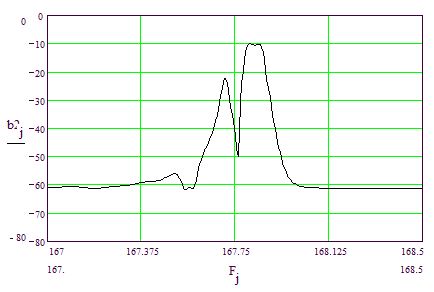
Рис.6. Расчетная характеристика АЧХ фильтра на 167,8 МГц при одинаковых периодах в ВШП и отражателях
Следует отметить, что наличие продольной моды также сильно сказывается на виде АЧХ в низкочастотной области полосы заграждения. При этом особая роль отводится точности воспроизведения величины зазора между ВШП и отражателем. На рис.7 показано, что изменением величины зазора на 5% от длины волны (0,9 мкм на данной частоте) можно снизить уровень продольной моды на 20 дБ. В реальном фильтре величина зазора была неоптимальной (17,5 мкм). Этим объясняется наличие пика в низкочастотной области полосы пропускания, рис.8.

Рис.7. Влияние величины зазора между ВШП и отражателем на АЧХ фильтра:
а) величина зазора равна 17,9 мкм; б) величина зазора равна 17,0 мкм
Экспериментальная характеристика фильтра, приведенная на рис.8, соответствует варианту с каскадным включением двух структур. Различие расчетной и экспериментальной характеристик в переходной области обусловлено разбросом центральных частот преобразователей, вызванных технологическими погрешностями. Анализ частотных уходов по шайбе ST-кварца диаметром 76 мм, изготовленной на основе стандартного (без подстройки частоты) технологического процесса, показал, что величина разброса соизмерима с шириной полосы пропускания фильтра (30 кГц).
Данная конструкция обеспечила уровень вносимого затухания 4,7 дБ (2,3 дБ на один каскад) в полосе пропускания 70 кГц. Следует отметить, что нагрузка 50 Ом не является оптимальной в данном случае. Это связано с физической природой STX-кварца (малая величина коэффициента связи), поэтому предпочтительно использовать более высокоомную нагрузку порядка 200 Ом. Практическая реализация таких условий возможна за счет использования схем трансформации сопротивления, описанных в работе [13].
Аналогичные результаты были получены на фильтрах с центральной частотой 157 МГц и 290 МГц: вносимое затухание при каскадном включении двух модулей не превышало 5 дБ в полосе пропускания 70 кГц и 120 кГц, соответственно [14].
Таким образом, фильтры на основе поперечно-связанной структуры являются наиболее узкополосными (не более 0,04%), что обусловлено природой используемого пьезоэлектрика (STX-кварц). При этом они позволяют обеспечить уровень вносимого затухания 2,3 дБ на один каскад.