Представлены результаты исследований основных СОМ-параметров (коэффициента отражения, коэффициента связи и эффективной скорости волны), как функции коэффициента металлизации в электродной структуре и толщины пленки алюминия, для ряда срезов пьезоматериалов, используемых в акустоэлектронике.

Важнейшими параметрами при проектировании устройств на поверхностных акустических волнах (ПАВ), в особенности фильтров с малым вносимым затуханием, являются коэффициент отражения от электрода и скорость акустической волны под электродной структурой. Тем не менее, существует мало публикаций, посвященных  исследованию их зависимости от геометрии электродной структуры (коэффициента металлизации решеток и толщины напыляемой пленки), что связано с большими трудностями измерения данных параметров.

В настоящей работе были экспериментально получены отражательные характеристики алюминиевых полосок и зависимость эффективной скорости ПАВ от параметров электродной структуры для пьезоэлектриков: 64°УХ-LiNbO₃, 41°УХ-LiNbO₃, 49°УХ-LiNbO₃, 128°УХ-LiNbO₃, выпускаемых российскими производителями. В качестве тестовой структуры для сильных пьезоэлектриков использовалась конструкция на основе продольно-связанной резонаторной структуры, для 128°УХ-LiNbO₃ -  структура, работающая на основе реверсивного МПО. Исследуемый диапазон по коэффициенту металлизации составлял km=0.3…0.5, по относительной толщине металлизации – hm=0.018…0,05, рис.1.  Методологический подход к обработке экспериментальных результатов был идентичен во всех случаях и основывался на методе полиномиальной регрессии второй степени. При этом величина погрешности не превышала 12%. Такая величина ошибки в большинстве случаев является допустимой, поскольку приводит к незначительному изменению амплитудно-частотной характеристики фильтра в части ширины полосы пропускания и положения центральной частоты.

Рассмотрим основные результаты исследований на примере данных по коэффициенту отражения Кр от пары закороченных алюминиевых полосок, нанесенных подложку из  64°УХ-LiNbO₃, рис.2.

На рис.3 приведена полученная зависимость коэффициента отражения Кр от коэффициента металлизации для диапазона относительной толщины металлизации 0,018…0,05λ. Шаг изменения hm равен 0,004λ. Анализ характеристик показывает, что существует значительная нелинейность в изменении коэффициента отражения с ростом толщины пленки. Этот эффект обусловлен изменением коэффициента связи  ΔV/Vпри нанесении тонких (меньше длины волны) пленок на поверхность пьезоэлектрика.

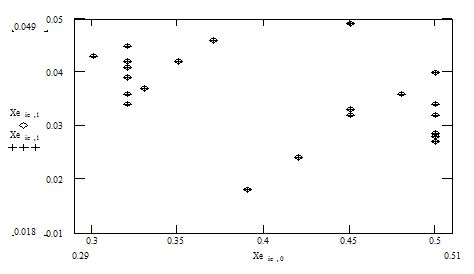
Рис.1. Положение экспериментальных точет коэффициента отражения для пары закороченных электродов для 64°LN в плоскости km, hm

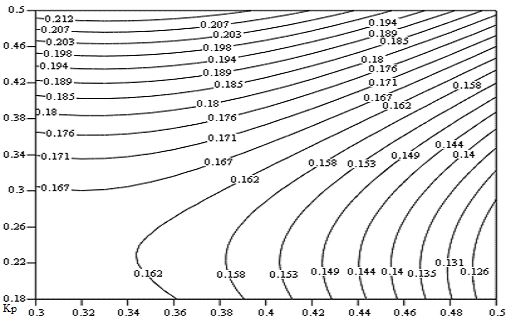
Рис.2. Распределение коэффициента отражения от пары закороченных электродов для 64°LN в плоскости km, hm, полученное методом полиномиальной регресии второго порядка

Рис.3. Зависимость расчетного коэффициента отражения Кр от коэффициента металлизации km для диапазона относительной толщины металлизации 0,18…0,05λ. Шаг изменения hm= 0,04λ

Представляет интерес сравнение полученных результатов с выводами Хартмана-Плесского-Райта [1,2] для 64°УХ-LiNbO₃. На рис.4 приведены расчетные кривые Кр, полученные на основании уравнения  [2]:

где  K  - коэффициент отражения на длину волны; h_λ-  толщина пленки в длинах волн;   Δ   -     коэффициент металлизации в структуре;    Ps - функции Лежандра, где s определяет тип электродной структуры (количество электродов на период); dV - коэффициент электро-механической связи; А₁, А₂ – числовые коэффициенты;  знак + соответствует случаю короткозамкнутых  полосок.

Рис.4. Зависимость коэффициента отражения от km, hm,
рассчитанная по выражению (1)

Из сравнения графиков рис.3,4 видно, что они различаются не только по абсолютной величине Кр, но и по характеру изменения коэффициента отражения от толщины пленки, который в последнем случае носит постоянный характер (постоянное приращение Кр при шаговом изменении толщины металлизации). Эта разница обусловлена тем, что:

1. Коэффициенты А_i сильно зависят от используемой технологии изготовления (плотности металла, степени клиновидности алюминиевой полоски по толщине, мощностных режимов напыления пленки, наличия примесей в используемой мишени и т.д.) и их величина может значительно меняться от типа технологического процесса. Подбором соответствующих значений данных коэффициентов можно скорректировать абсолютную величину Кр до реальных экспериментальных значений.
2. Второе отличие носит принципиальный характер, поскольку связано с изменение dV в плоскости hm, km. Данный эффект не учитывается в выражении (1).

В данной работе получено уточненное выражение для Кр, обеспечивающее большую сходимость теоретических и экспериментальных результатов (2):

На рис.5 приведена величина погрешностей расчетных значений Кр, полученных по (1) и (2). Максимальная величина ошибки в первом случае составляет 21%, во втором  - 14%. Следует отметить, что реальная величина dV также отличатся от расчетного значения 0,0465 и составляет величину порядка 0,063.

Рис.5. Величина погрешности Кр (в процентах)
при использовании выражений (1) - □ и (2) - 

Для анализа изменения dV в плоскости hm, km была применена полиномиальная регрессия первого порядка. При этом получено, что абсолютная величина изменения dVв исследуемом диапазоне hm, km  составляет 5%.

Аналогичный подход был использован при обработке экспериментальных результатов по коэффициенту отражения и эффективной скорости волны для 64°УХ-LiNbO₃ , 41°УХ-LiNbO₃ , 49°УХ-LiNbO₃ и 128°УХ-LiNbO₃. В результате которого были получены следующие аналитические выражения для основных СОМ-параметров (3):

где    K  - коэффициент отражения на длину волны; V–   эффективная скорость под электродной структурой;  V_o  - скорость ПАВ на свободной поверхности; h_λ -  толщина пленки в длинах волн; Δ -     коэффициент металлизации в структуре;   Ps  -функции Лежандра, где s определяет тип электродной структуры (количество электродов на период); dV - коэффициенты электро-механической связи; А, В – числовые коэффициенты;  знак ±   соответствует случаям короткозамкнутых либо разомкнутых полосок.

В таблице  приведены данные по чувствительности эффективной скорости волны  различных срезов к величине коэффициента металлизации структуры в диапазоне частот 100…800 Мгц для закороченных алюминиевых полосок  (толщина металлизации 0,3 мкм).

Использование  полученных зависимостей для коэффициента отражения и эффективной скорости волны при разработке ПАВ-фильтров с малыми потерями позволило уменьшить число расчетных итераций до 1-2 и разработать систему рекомендуемых допусков на основные технологические операции, что обеспечило увеличение процента выхода годных на 20% при серийном внедрении ПАВ-фильтров в производство.

Таблица. Влияние коэффициента металлизации на величину эффективной скорости волны 

Список литературы

1. Hartmann C., Plessky V., Experimental measurement of propagation, attenuation, reflection and scattering of leaky waves in Al electrode gratings on 41°, 52° and 64°-lLiNbO₃ // IEEE Ultrason. Symp. Proc., 1994 p.120-123
2. Wright P., Modeling and experimental measurements of the reflection properties of SAW metallic gratings // IEEE Ultrason. Symp. Proc., 1984, p.54-63